[수학] 순열, 조합 공식 총정리
- ETC.
- 2020. 9. 12.
팩토리얼 ( ! )
팩토리얼이란 서로 다른 n개를 나열하는 경우의 수를 의미합니다. 기호로는 n! 이렇게 쓰고 계산은 n부터 1씩 줄여나가면서 1이 될때까지의 모든 수를 곱합니다.
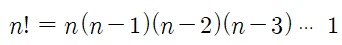
순열 ( nPr )
순열이란 서로 다른 n개중에 r개를 선택하는 경우의 수를 의미합니다. (순서 상관 있음)
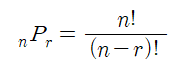
조합 ( nCr )
조합이란 서로 다른 n개중에 r개를 선택하는 경우의 수를 의미합니다. (순서 상관 없음)
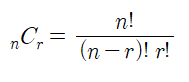
중복 순열 ( nπr )
중복 순열이란 중복 가능한 n개중에서 r개를 선택하는 경우의 수를 의미합니다. (순서 상관 있음)
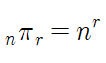
중복 조합 ( nHr )
중복 조합이란 중복 가능한 n개중에서 r개를 선택하는 경우의 수를 의미합니다. (순서 상관 없음)
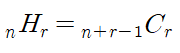
같은 것이 있는 순열
순열이 같은 것이 포함된 원소들을 나열하는 경우의 수는 나열하는 원소의 팩토리얼에 중복된 원소들의 팩토리얼을 나누어주면 됩니다.
예를 들어 aaabb와 같은 경우 a가 3개이고 b가 2개이므로 5!을 3!와 2!로 나누어주면 됩니다.
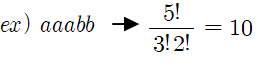
원 순열
원 순열은 원 모양의 테이블에 n개의 원소를 나열하는 하는 경우의 수입니다.

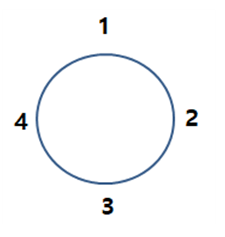
예를 들어 원 모양의 테이블에 4명을 앉힐려고 한다면
1에서 시작해서 1234로 앉히던
2에서 시작해서 2341로 앉히던
3에서 시작해서 3412로 앉히던
4에서 시작해서 4123로 앉히던
원을 돌리면 모두 같다고 봅니다.
그렇기에 4팩토리얼을 4로 나누어준다면 아래와 같은 결과값을 얻을 수 있습니다.
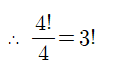
염주 순열
n개의 서로 다른 종류의 구슬로 목걸이를 만드는 경우의 수
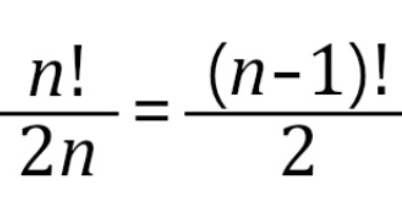
원순열과 비슷하지만 목걸이는 뒤집어도 같은 것으로 취급하므로 2배가 중복됩니다.
최단거리 경우의 수
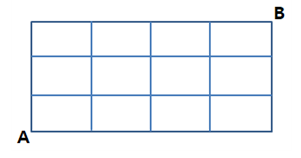
A에서 B까지의 최단거리로 가는 경우의 수를 구하는 방법을 구하는 방법은 2가지가 있습니다.
A에서 B까지 최단거리로 가려면 무조건 위로 3번 오른쪽으로 4번을 가야합니다.
그렇기에 7개를 나열하는 것이니 7! 을 분자로 두고 오른쪽으로 4! 위쪽으로 4!을 나누어주는
아래와 같은공식을 도출하여 구하는 방법이 있고
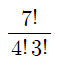
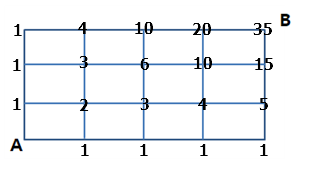
위와 같이 합의 법칙을 통해 구하는 방법이 있습니다.
집합의 분할 S(n, k)
집합의 분할이란 서로 다른 n개를 똑같은 상자 k개에 넣는 경우의 수를 의미합니다. (빈상자는 있으면 안됌)]
ex) 서로 다른 6개의 공을 똑같이 생긴 2개의 상자에 넣는 경우의 수
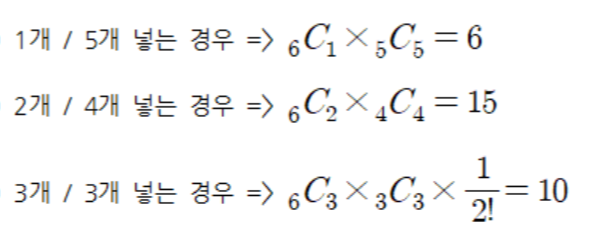
6개를 똑같이 생긴 2개의 상자에 넣는 경우의 수는 6+15+10 = 31가지입니다.
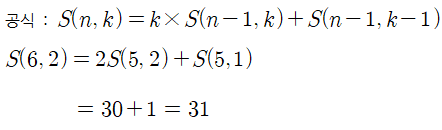
위와 같이 공식을 통해서 구할 수도 있습니다.
자연수의 분할 P(n, k)
자연수의 분할이란 똑같은 n개를 똑같이 생긴 상자 k개에 넣는 경우의 수를 말합니다. (빈상자는 있으면 안됌)
ex) 서로 같은 6개의 공을 똑같이 생긴 2개의 상자에 넣는 경우의 수

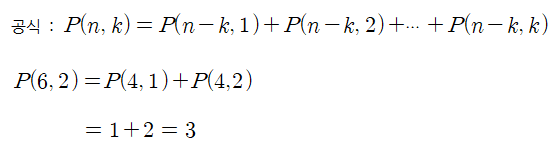
이항 정리
이항정리란 (a+b)의 n승을 전개한것을 이항정리라고 합니다.
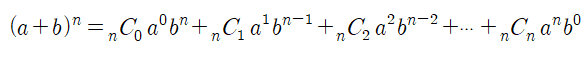
이항 정리의 파생 공식
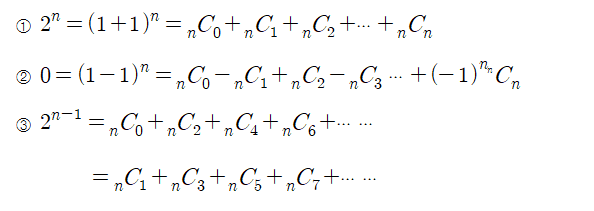
순열과 조합 알고리즘 구현
'ETC.' 카테고리의 다른 글
| [수학] 보수 계산법 (1의보수, 2의보수) + 필요한 이유 (1) | 2021.01.27 |
|---|---|
| [수학] 진법 변환 방법 정리 + 소수점 (2진수, 8진수, 10진수, 16진수) (2) | 2021.01.27 |
| [ETC] 코딩을 잘하는 사람들의 특징 (28) | 2019.12.30 |
| [기타] 매크로 프로그래밍에 대해서 (1) | 2019.02.02 |