[Algorithm] 에라토스테네스의 체 - 소수 구하기 (범위)
- ETC./Algorithm
- 2020. 9. 6.
에라토스테네스의 체란?
고대 그리스의 수학자 에라토스테네스가 만들어 낸 소수를 찾는 방법이며 이 방법은 마치 체로 치듯이 수를 걸러낸다고 하여 '에라토스테네스의 체'라고 부릅니다. 특정 숫자의 배수는 소수가 아니라는 법칙에 착안하여 2 ~ N까지의 숫자에서 숫자들의 배수를 모두 제거한 뒤 제거되지 않은 숫자를 소수로 판별하는 방식이며 일종의 노가다 방식이라 상당히 무식한 방법이지만 이 방식이 프로그래밍에서는 상당히 효율적인 방법론이 됩니다. 에라토스테네스의 체는 반대로 2부터 배수들을 지워나가는 방식이기 때문에 숫자마다 일일이 약수가 있는지 검사할 필요가 전혀 없고, 이미 지워진 숫자는 바로 건너뛰면 되니 실행시간이 매우 짧습니다.
특정 범위에서의 모든 소수를 찾을때 가장 효율적인 알고리즘
에라토스테네스의 체는 특정 범위가 주어지고 그 범위 내의 모든 소수를 찾아야 하는 경우에 가장 좋은 효율을 보입니다. 만약, 대량의 소수를 한꺼번에 판별해야 할 경우는 '에라토스테네스의 체'를 이용하면 가장 빠른 속도로 소수들을 찾을 수 있습니다. 이때 시간 복잡도는 O(N log long N)입니다.
특정 숫자에 대한 소수 판별은 에라토스테네스의 체를 활용하기에는 필요없는 숫자들의 소수 판별도 자연스럽게 해야 하다 보니 숫자가 커지면 커질수록 비효율적입니다. 특정 숫자에서의 소수 판별은 그냥 2~루트 N까지의 for문을 돌리면서 특정 숫자의 제곱근까지만 약수의 여부를 검증하면 O(N^1/2)의 시간 복잡도로 빠르게 구할 수 있습니다.
예제 2 ~ 120 까지의 모든 소수 찾기
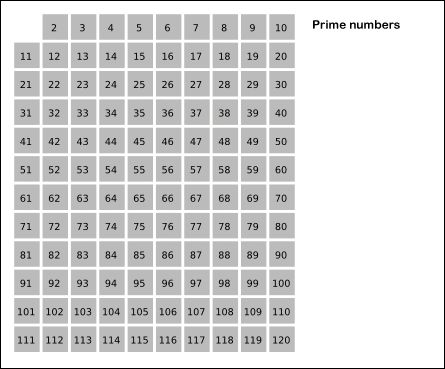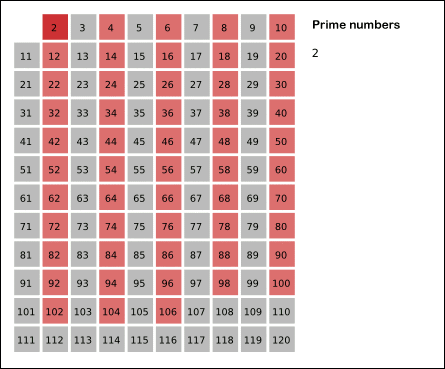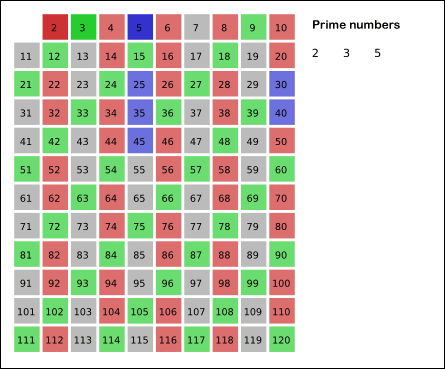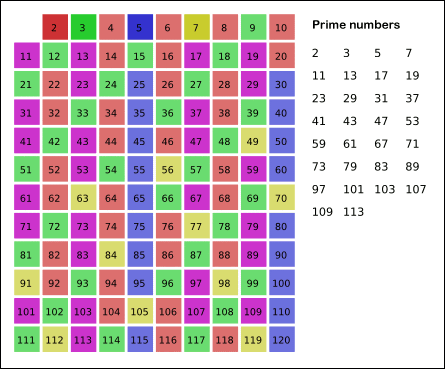
과정
1. 2 ~ 120까지의 모든 숫자들을 나열합니다.
2. 2는 소수이므로 오른쪽에 2를 쓰고 2의 배수들을 모두 지웁니다. (빨간색)
3. 남아있는 숫자에서 3은 소수이므로 오른쪽에 3을 쓰고 3의 배수들을 모두 지웁니다. (초록색)
4. 남아있는 숫자에서 5는 소수이므로 오른쪽에 5를 쓰고 5의 배수들을 모두 지웁니다. (파란색)
5. 남아있는 숫자에서 7는 소수이므로 오른쪽에 7을 쓰고 7의 배수들을 모두 지웁니다. (노란색)
6. 위의 과정을 반복합니다.
7. 11 ×11 은 121 로 범위 2 ~ 120을 넘기 때문에 반복을 멈추고 남은 수(소수)들을 출력합니다.
구현 (C / C++)
#include <stdio.h>
//범위의 소수 판별
void find_primeNumber(int target) {
bool arr[target+1]; // 숫자를 지울 배열
arr[0] = true;
arr[1] = true;
// 2부터 특정 수의 배수에 해당하는 수를 모두 지움
for(int i=2;i<=target;i++) {
if(arr[i]) continue; // 이미 지워진 수라면 건너뜀
// 이미 지워진 숫자가 아니라면, 해당 숫자의 배수를 모두 true로 만듦
for(int j=2*i;j<=target; j+=i) {
arr[j] = true;
}
}
// 남아있는 수를 모두 출력 (배열에서 false인 index)
for(int i=2;i<=target;i++) {
if(!arr[i]) printf("%d ", i);
}
}
int main(void) {
find_primeNumber(120); //120까지
return 0;
}

'ETC. > Algorithm' 카테고리의 다른 글
| [Algorithm] 알고리즘 시간복잡도에 대하여 (4) | 2020.09.14 |
|---|---|
| [Algorithm] 순열 조합 알고리즘 개념과 예제 (구현) (0) | 2020.09.13 |
| [Algorithm] 유클리드 호제법 - 최대공약수(GCD) 구하기 (0) | 2020.09.05 |
| [Algorithm] 이진탐색 알고리즘 (0) | 2019.07.08 |