순열과 조합 실생활 예
순열과 조합의 차이는 순서를 정하느냐 그렇지 않느냐의 차이입니다.
순열 : 중국집 메뉴 5개 중 2개의 메뉴를 순서대로 먹는 경우의 수
조합 : 중국집 메뉴 5개 중 2개의 메뉴를 주문하는 경우의 수
순열이란?
순열이란 서로 다른 n개중 r개를 골라 순서를 고려해 나열한 경우의 수를 말합니다.
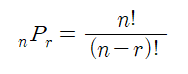
예를 들어 어느 중국집에 5개의 메뉴(a,b,c,d,e)가 있다고 해봅시다. 이때 5개의 메뉴(a,b,c,d,e)중 2개의 메뉴를 순서대로 먹는 경우의 수는 몇가지가 있을까요? 먼저 첫번째로 먹을 메뉴를 정하려면 이때 첫번째 메뉴가 될 수 있는 경우의 수는 5가지 입니다. 그리고 나서 첫번째 메뉴로 지정된 메뉴를 제외한 나머지 4가지의 메뉴로 두번째로 먹을 메뉴를 선택한다고 가정하면 이때의 경우의 수는 4가 됩니다. 그러므로 5개의 메뉴 중 2개의 메뉴를 차례대로 먹을 경우의 수는 20(5X4)가지 입니다. 이때 메뉴는 a와 b를 결정하였다고 한다면 a,b가 될수도 있고 b,a가 될수도 있습니다. 먹는 순서가 다르기에 a,b와 b,a는 엄연히 다른 경우이며 순서를 고려한다는것은 이러한 의미입니다.
순열 알고리즘 구현 (C++)
#include<iostream>
#include<vector>
#define MAX 5
using namespace std;
char Arr[MAX];
bool Check[MAX];
vector<char> V;
void Permutation(int n, int r)
{
if (n == r)
{
for (int i = 0; i < V.size(); i++)
{
cout << V[i] << " ";
}
cout << endl;
return;
}
for (int i = 0; i < MAX; i++)
{
if (Check[i] == true) continue;
Check[i] = true;
V.push_back(Arr[i]);
Permutation(n+1 , r);
V.pop_back();
Check[i] = false;
}
}
int main(void)
{
Arr[0] = 'a';
Arr[1] = 'b';
Arr[2] = 'c';
Arr[3] = 'd';
Arr[4] = 'e';
Permutation(0,2);
}

조합이란?
조합이란 서로 다른 n개중에 r개를 선택하는 경우의 수를 의미합니다.

예를 들어 어느 중국집에 5개의 메뉴(a,b,c,d,e)가 있다고 해봅시다. 이때 5개의 메뉴(a,b,c,d,e)중 2개의 메뉴를 주문하는 경우의 수는 몇가지가 있을까요? 먼저 첫번째 메뉴의 선택하려면 경우의 수는 5가지 입니다. 그리고 나서 첫번째 메뉴로 지정된 메뉴를 제외한 나머지 4가지의 메뉴로 두번째로 먹을 메뉴를 선택한다고 가정하면 이때의 경우의 수는 4가 됩니다. 그러므로 5개의 메뉴 중 2개의 메뉴를 주문하는 경우의 수는 20(5X4)가지 입니다. 이때 메뉴는 a와 b를 결정하였다고 한다면 a,b가 될수도 있고 b,a가 될수도 있습니다. 하지만 a,b와 b,a는 서로 같기에 나누기 2!을 해주어 메뉴 5개중 2개의 메뉴를 주문할 확률은 10(5X4/2)이 됩니다.
조합 알고리즘 구현 (C++)
#include<iostream>
#include<vector>
#define MAX 5
using namespace std;
char Arr[MAX];
bool Check[MAX];
vector<char> V;
void combination(int idx, int n, int r)
{
if (n == r)
{
for (int i = 0; i < MAX; i++)
{
if (Check[i] == true)
{
cout << Arr[i] << " ";
}
}
cout << endl;
return;
}
for (int i = idx; i < MAX; i++)
{
if (Check[i] == true) continue;
Check[i] = true;
combination(i,n+1,r);
Check[i] = false;
}
}
int main(void)
{
Arr[0] = 'a';
Arr[1] = 'b';
Arr[2] = 'c';
Arr[3] = 'd';
Arr[4] = 'e';
combination(0,0,2);
}

좀 더 다양한 순열과 조합의 공식을 보고싶다면 아래 링크를 클릭해주세요.
'ETC. > Algorithm' 카테고리의 다른 글
| [Algorithm] 알고리즘 공간복잡도에 대하여 (0) | 2020.09.15 |
|---|---|
| [Algorithm] 알고리즘 시간복잡도에 대하여 (4) | 2020.09.14 |
| [Algorithm] 에라토스테네스의 체 - 소수 구하기 (범위) (2) | 2020.09.06 |
| [Algorithm] 유클리드 호제법 - 최대공약수(GCD) 구하기 (0) | 2020.09.05 |