진법이란?
진법이란 수를 표기하는 기수법의 하나로 몇 개의 기본 숫자를 이용하여 수를 표시하는 방법입니다. 자리값이 올라감에 따라서 수가 일정하게 커지는 규칙을 이용하고 수를 표시합니다. 우리가 일반적으로 사용하는 1 ~ 9까지의 숫자를 사용하여 수를 나타내는 방법을 10진법이라고 하며 프로그래밍에서 주로 사용되고 있는 진법은 아래와 같습니다.
위치의 가중치

모든 진법은 숫자의 위치에 따라 가중치가 달라지는 수입니다. 이 성질은 모든 진법에서 동일하게 적용되며 이 식을 사용하면 모든 진법들을 10진법으로 빠르게 바꿀 수 있습니다. 위의 경우 12345라는 10진법이 나오기 아래와 같은 식이 구해져야합니다.
계산식 : (1 * 10⁴) + (2 * 10³) + (3 * 10²) + (4 * 10) + 5 = 12345
컴퓨터 학문에서 주로 사용하는 진법은 아래와 같습니다.
1. 2진법
2. 8진법
3. 10진법
4. 16진법
이번 포스팅에서는 진법끼리 서로 변환시키는 방법에 대해 알아보도록 하겠습니다.
10진수를 X진수로 변환
정수 부분

바꾸고 싶은 진수의 숫자로 더 이상 나눌 수 없을 때까지 나눈 뒤 역순으로 읽으시면 됩니다. 25를 각각 2진법, 8진법, 16진법으로 변환하면 위와 같은 결과가 나오게 됩니다.
소수 부분

소수 부분은 바꾸고 싶은 진수를 소수점 밑에 모두 0이 될때까지 계속 곱해주면 됩니다. 0.25를 각각 2진법, 8진법, 16진법으로 변환하면 위와 같은 결과가 나오게 됩니다.
X진수를 10진수로 변환
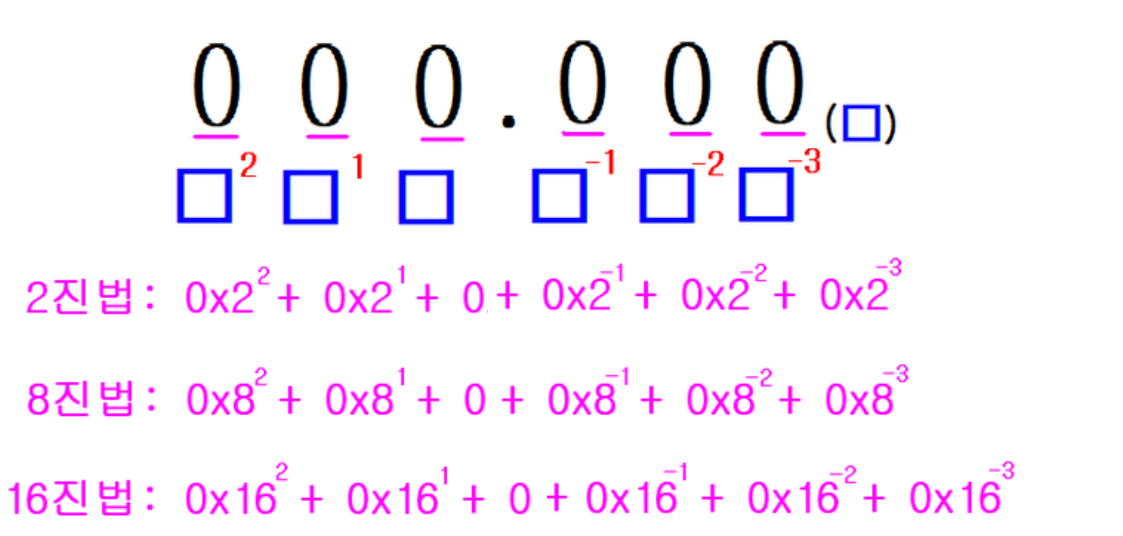
변환하려는 진수의 각 자리 값과 각 자리의 지승의 승을 곱한 후에 모두 더해주면 됩니다.

2진수를 8진수, 16진수로 변환

2진수를 8진수 16진수로 변환할때 소수점을 기준으로 좌우로 8진수는 3자리씩, 16자리는 4자리씩 끊어주고 빈자리는 0으로 채워주면 됩니다.
'ETC.' 카테고리의 다른 글
| [수학] 초 단위 종류 (극 미세 시간) + 변환 사이트 (0) | 2021.02.18 |
|---|---|
| [수학] 보수 계산법 (1의보수, 2의보수) + 필요한 이유 (1) | 2021.01.27 |
| [수학] 순열, 조합 공식 총정리 (10) | 2020.09.12 |
| [ETC] 코딩을 잘하는 사람들의 특징 (28) | 2019.12.30 |